Math Definition Of Irrational Number
Incredible Math Definition Of Irrational Number 2022. Many people are surprised to know that a repeating decimal is a rational. An irrational number is hence, recurring numbers.
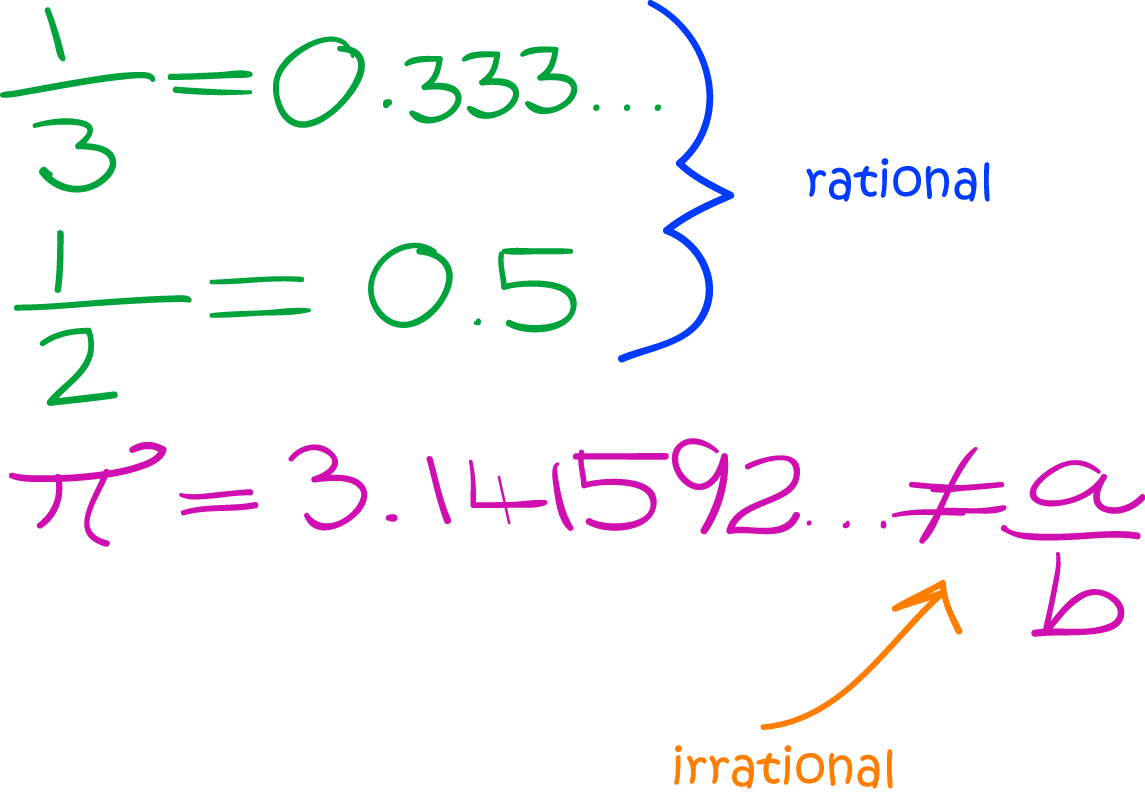
A number is irrational if. Usually, we say that it is a number that it is not rational. An “irrational number” is a real number that cannot be expressed as a simple fraction for any integers.
In Math, However, It Has A Different, More Technical Definition.
An irrational number is hence, recurring numbers. Usually, we say that it is a number that it is not rational. Irrational numbers are the set of real numbers that cannot be expressed in the form of a fraction p/q where p, q are integral values.
Rational Numbers, On The Other Hand, Can Be Split Into Rational Numbers With Repeating Decimals And.
A ratio nal number is one that can be written as the ratio of two integers. Irrational means not rational (no ratio). P can be a positive, negative, or even a zero integer.
What Is A Formal Definition Of A Irrational Number?
A number that cannot be expressed as the ratio of two integers. Irrational means no ratio, so it isn',t a rational number. In mathematics, the word has a completely different meaning,
Quality Learning Support For All
Irrational numbers have decimal expansions that neither terminate nor become. Here are some of the most common irrational numbers that you’ll encounter in your math classes and even advanced classes in. When an irrational number is written with a decimal point, the numbers after the.
1.5 Is Rational, But Π Is Irrational.
An integer has no fractions.) its decimal goes on forever without repeating. A real number that can not be made by dividing two integers (an integer has no fractional part). An irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q.
Post a Comment for "Math Definition Of Irrational Number"